小学生のときに算数を教えてくれたタカハラ先生が素晴らしく高度だった件
小学生のときに算数を教えてくれた先生のお話です。
算数の時間

わたしが小学5,6年生のときでした。小学校なので、授業は基本的に全て担任の先生が担当します。
わたしは4組で、担任の先生は音楽の先生でした。2組の担任の先生はタカハラ先生という男の先生でした。
とある頃から、算数の時間はタカハラ先生が授業をするようになりました。その時間、2組では音楽の授業が行われていたようです。つまり、算数と音楽の時間を合わせて、担任が交代していたんです。
なぜそういうことをしていたのかは、知りません。分かりますけど、知りません。はい。
扇形の面積
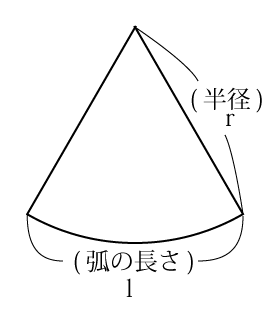
扇形の面積は、中心角を とするとき、円の面積に
をかけて、割合で算出するのが初歩的なやり方です。
高校で弧度法を学習すると、半径を 、この長さを
とするとき
で求めることができるようになります。
タカハラ先生は、これをわたしたちに教えてくれました。
扇形をゼリーだと思え
いいか、扇形をプルンップルンのゼリーだと思うんだ。このゼリーを、横に何回も切るんだ。
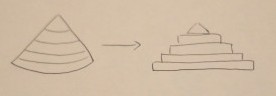
切ったら、ゼリーは重いからボトッと落ちるだろ。4,5回切ったくらいだったら、上の図みたいにガタガタの段差で重なるよな。
これを、頭のなかで何千回も何万回も切ったら、段差はほとんど無くなるよな。
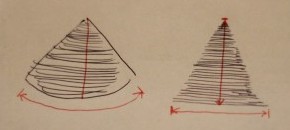
段差がなくなれば、上の図みたいに三角形に近くなるよな。
ボトッと落ちると、両端の2辺の長さは半径よりも長くなってしまう。でも、下の弧の長さは底辺の長さと変わらないし、中心から一番下までの半径の長さはそのまま高さで変わらないだろ。(図の赤い線の部分)
だから、この扇型の面積は、切り刻んだあとの三角形の面積と同じなんだ。
底辺は弧の長さ。高さは半径と同じだから、(弧長)×(半径)÷2で面積が出るんだよ。
成長してから分かるこの凄さ
数学奇人のみなさんは、もうお分かりですね。すごくないですか、この先生。
積分ですよ。完全に積分の考え方です。小学生相手に、こんなに分かりやすく積分を説明してくれたんです。
これって、完全に子どもたちは理解し、頭に残ってますよ。ここに生き証人がいます。三十数年前に習ったことを、昨日習ったことのように思い出せます。
「わかる」と「できる」は違いますが、子どもは分かるとモチベーションが上がるのは間違いありません。
わたしは生徒に対して「分かる」そして「印象に残る」授業をすることができているんでしょうか。
タカハラ先生のことを思い出す度に、自分の未熟さを反省させられます。





