30日間1日1本マクロ生活、ついに30日目です。
マクロを書く準備は、0日目に記事を書きました。
トーナメント表の作成
実はこのブログで、以前にトーナメント表の作成を記事にしたことがありました。
いつものように、そのまま放置してしまったんですが、今回やっとケリをつけることができそうです。
ただ、上の記事に書かれている「WordPressで表示させる」までは今回はできそうにありません。
需要があれば、またの機会に紹介できればと思っています。
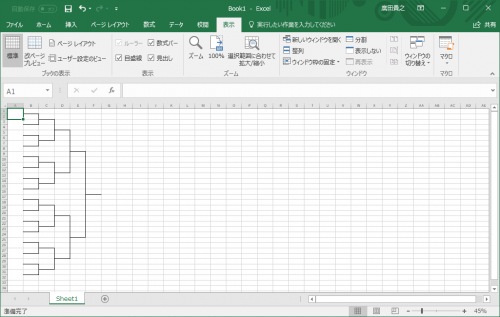
とりあえず、こんなトーナメント表を作ることを目標とします。
セルの結合
上の記事にもあるんですが、トーナメント表を作るとき、選手(またはチーム)の名前が入っているセルの真ん中から勝ち上がりの線が出るようにしなければなりません。
このため、選手名(チーム名)を入れるセルは2つのセルを結合させて使います。
こんな感じにするんです。
セルを結合させる命令は「Merge」です。
「Range(Cells(1,1),Cells(2,1)).Merge」とすると、A1とA2が結合されて1つのセルみたいになります。
Sub マージ(k)
For n = 1 To k
Range(Cells(2 * n - 1, 1), Cells(2 * n, 1)).Merge
Next n
End Sub
「マージ」というマクロを書いてみました。
kに出場者数を入れると、結合されたセルが人数分作られます。
トーナメント表のしくみ
トーナメント戦って、基本的に1人対1人、1チーム対1チームで対戦して、勝った方が上がりますよね。
だから、4人が参加するトーナメント戦だったら1回戦は2試合、2回戦が決勝戦です。
6人が参加するトーナメント戦だったら、2人、2人、2人の6人が1回戦を戦う。1回戦は3試合です。そして、残った2人が1回戦は不戦勝。2回戦からの登場です。
2人で戦うのが基本なので、トーナメント表の1回戦は 人が参加する形になっているのが最も基本的な形と言えます。
だから、出場選手は2人、4人、8人、16人、32人、・・・を基本に考え、それに足りない分が不戦勝になるというのがトーナメント戦の考え方です。
とりあえず15人で
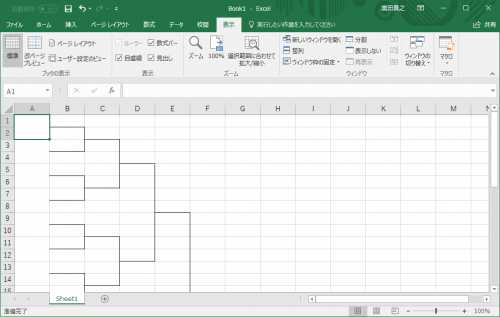
とりあえず、今日は15人のトーナメント表を考えましょう。
ですから、16人のトーナメント表を作って、1人不戦勝です。
2の何乗?
ベースとなる「16」が2の何乗になるのかがとても大切です。
16は2の4乗です。だから、このトーナメント表は4回戦まであります。4回戦が決勝戦です。
256人が参加するトーナメント戦は、256が2の8乗なので8回戦まであります。
高校柔道の最大の大会である金鷲旗高校柔道大会は、2017年の大会では男子の参加校が322校、女子は168校でした。
2の8乗が256、2の9乗が512なので、322校が参加するトーナメント戦の決勝戦は9回戦です。
何故この数字が大切かというと、トーナメントの山を何段積み上げていくのかが分からなければ、山が組めないからです。
Function ninobeki(n)
If n < 1 Then Exit Function
If n = 1 Then
ans = 0
Else
ans = 1
Do Until n <= 2 ^ ans
ans = ans + 1
Loop
End If
ninobeki = ans
End Function
「ninobeki」という関数を作ってみました。
t=1から始めて、2のt乗が人数を超えるまでループを繰り返せば、その人数を超える最初の2のt乗が分かるという仕組みです。
山組みをはじめよう
実際に山組みをはじめます。
箱の真ん中から勝ち上がりの線を出し、隣の勝ち上がりの線とつなぐ。これを山の一番上まで繰り返すだけです。
1回戦だけなら全ての箱の真ん中から線を出すコードを書けばいいんですが、これだと同じようなコードをいくつもいくつも書くことになり、マクロの意味が薄れちゃいます。
「n回戦ならどうなるか」を考え、全ての場合に対応できるようなマクロを書いてこそ美しい。
ということで、苦労してみました。
For n = 1 To d
m = 2 ^ (i - 1) * (2 * n - 1)
y1 = m - 2 ^ (i - 2) + 1
y2 = m + 2 ^ (i - 2)
Call rtb(y1, y2, x)
Next n
「i回戦」の場合です。
例えば1回戦の第1試合は、セルの1段目から4段目までに箱が書いてあります。
1回戦の第2試合は5段目から8段目までです。第3試合は9段目から12段目。
つまり、1回戦は1つの試合に4段ずつ使うということです。
2回戦は1つの試合に8段を使います。3回戦は16段です。
それらの真ん中の段から、それぞれの勝ち上がりの線までいくつ上がるか、いくつ下がるかを考えると、上のようなコードになりました。
このコードを書くのに、試行錯誤を繰り返して、1時間半ほどかかっちゃいました。まだまだ未熟です。
「Next n」の上にある「rtb」は、セルの右と上と下に線を引くというコマンドを自作したものです。
Sub rtb(y1, y2, x)
Set r = Range(Cells(y1, x), Cells(y2, x))
r.Borders(xlEdgeTop).LineStyle = 1
r.Borders(xlEdgeBottom).LineStyle = 1
r.Borders(xlEdgeRight).LineStyle = 1
End Sub
見慣れない表記もあるかと思いますが、需要があれば説明したいと思います。
これらを駆使して、ついに出来上がったのが次のコードです。
これが完成
Sub 山組()
Cells.Delete
ninzu = 15
b = ninobeki(ninzu)
bas = 2 ^ b
Call マージ(bas)
For i = 2 To b + 1
d = 2 ^ (b - i + 1)
x = i
For n = 1 To d
m = 2 ^ (i - 1) * (2 * n - 1)
y1 = m - 2 ^ (i - 2) + 1
y2 = m + 2 ^ (i - 2)
Call rtb(y1, y2, x)
Next n
Next i
Cells(bas, x + 1).Borders(xlEdgeBottom).LineStyle = 1
End Sub
Function ninobeki(n)
If n < 1 Then Exit Function
If n = 1 Then
ans = 0
Else
ans = 1
Do Until n <= 2 ^ ans
ans = ans + 1
Loop
End If
ninobeki = ans
End Function
Sub rtb(y1, y2, x)
Set r = Range(Cells(y1, x), Cells(y2, x))
r.Borders(xlEdgeTop).LineStyle = 1
r.Borders(xlEdgeBottom).LineStyle = 1
r.Borders(xlEdgeRight).LineStyle = 1
End Sub
Sub マージ(k)
For n = 1 To k
Range(Cells(2 * n - 1, 1), Cells(2 * n, 1)).Merge
Next n
End Sub
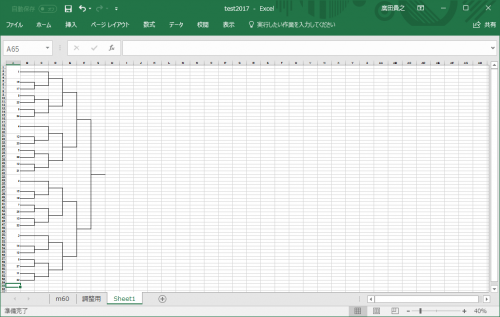
実行結果
実行結果は、最初に示したトーナメント表です。
実際には、「ninzu」の数字を変えることで、好みの出場者数のトーナメント表を作ることが可能です。
ただし、今回は出場者数を超える最小の2の○乗が出場する山組みが出せるだけです。
実は、2の○乗でない場合は不戦勝の人が2回戦に勝ち上がっているようなトーナメント表を作るマクロは出来上がってます。
ただ、それをここで説明するにはあまりにも長くなりすぎます。
需要があれば、ご紹介したいと思ってます。
こんな感じです。どうでしょう。
ついに完走!
30日間1日1本マクロ生活、ついに完走しました。
いやあ、1か月間、ずっと同じようなことを書き続けたんですけど、かなり心が折れそうでした。
だって、かなり反応が悪いんですもん。完全に自己満足の30日間でした
ただ、これを書いて記事にしておいておくことで、誰かが見て参考にしてくれるかもしれません。
わたし自身がマクロを人から習ったことがなく、全てはネットで検索して、誰かが書いたものを参考にして勉強してきたんですよね。
ですから、どんな小さなことでも、どんな簡単なことでも、ネット上に書いてあることってすごくありがたいんです。
「おもしろい」と思ってもらえる記事ではありませんでした。はっきり言って。
でも、置いておけば何かの価値になるかもしれないので。
Excelは便利
悔しいですが、Excelは便利です。
Microsoftにお金を払うのは癪でしょうがないんですが、Excelばかりは仕方がない。
マクロを書くようになると、Excelからは離れられないですね。
30日間、何とか頑張りました。ありがとうございました。