17日目 約分しよう【30日間1日1本マクロ生活】

30日間1日1本マクロ生活、17日目です。
マクロを書く準備は、0日目に記事を書きました。
約分
分数の計算って、小学校で習う算数の結構大きな壁だったりしませんでしたか?
分数って、結構高度なんですよ。小学校の先生がみんな分数の仕組みを本当に理解して教えているとはとても思えないです。
今日はそんな分数の「約分」についてやっていきます。
約分って、要は昨日やった「最大公約数」で分母と分子を割るってことですよね。
ですから、昨日作ったgcd関数を使って、「gcd(分子,分母)」で約分できる数を求めてしまえば、あとは割るだけ。
今日は簡単に終わりそうですね。
さっそくコードを
まずは昨日のgcd関数を。
Function gcd(m, n)
If m >= n Then
a = m
b = n
Else
a = n
b = m
End If
Do Until b < 1
r = a Mod b
a = b
b = r
Loop
gcd = a
End Function
そして、約分をするマクロです。
Sub yakubun()
shi = Cells(1, 1)
bo = Cells(2, 1)
yaku = gcd(shi, bo)
Cells(1, 3) = shi / yaku
Cells(2, 3) = bo / yaku
End Sub
解説します。
やっていることは単純です。
変数shiには、セルA1に入っている数を格納します。
変数boには、セルA2に入っている数を格納します。
それぞれ、分子、分母という設定です。
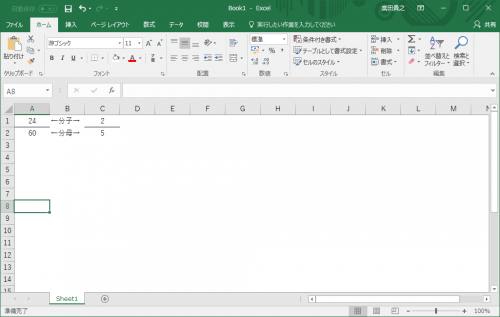
変数yakuに最大公約数を格納し、C1とC2に分子と分母をyakuで割った数をそれぞれ書き込みます。
約分って、これだけのことなんですよね。つまり、最大公約数が求められれば、割るだけなんです。
実行結果
マクロを記述するウィンドウの「Sub」と「End Sub」の間にカーソルを置いて、画面上方の再生ボタン的なアイコン(右向きの三角形)をクリックするか、[F5]キーを押して実行します。
はい、確かに約分されました。
Excelは便利
悔しいですが、Excelは便利です。
Microsoftにお金を払うのは癪でしょうがないんですが、Excelばかりは仕方がない。
マクロを書くようになると、Excelからは離れられないですね。
30日間、頑張ります。
マイクロソフト 2014-10-17