20日目 区分求積法【30日間1日1本マクロ生活】

30日間1日1本マクロ生活、20日目です。
ついに3分の2です。あと10日ですね。頑張ります。
マクロを書く準備は、0日目に記事を書きました。
区分求積法
今日は積分のお話です。
を計算すると、答えは
です。
この積分の計算をここで解説するのはやめておきますね。
一方、高校の数学IIIの教科書に載っている「区分求積法」という計算法があります。
というものです。
これがどういう意味なのか、ということも説明するのはやめておきますね。
いっぱい足し算したら円周率が求められる
この式の意味する所は、 がめっちゃ大きな数だったとして
という足し算をず~~~~~~~っとやっていって、その合計をnで割ったら、計算結果が円周率 の4分の1に近づいていくということなんです。
がどのくらい大きな数かって?百万?一億?
いやいや、そんなもんじゃないです。
なんたって無限大ですから。
だから、こんな計算、人間様の「手」でできるはずないんです。
だから、こんな時こそ機械の出番です。
Excelのマクロにやってもらいましょう。
さっそくコードを
Sub 区分求積()
s = 0
n = 10 ^ 8
For k = 1 To n
s = s + 1 / (1 + (k / n) ^ 2)
Next k
Cells(1, 1) = 4 * s / n
End Sub
解説します。
とりあえず、 は
とします。1億ですね。小さい数です。
変数sに足し算の結果をどんどん追加していきます。
最後にセルA1に合計のsを4倍してnで割ったものを表示します。
上手くいけば、これが に近い値になるはずです。
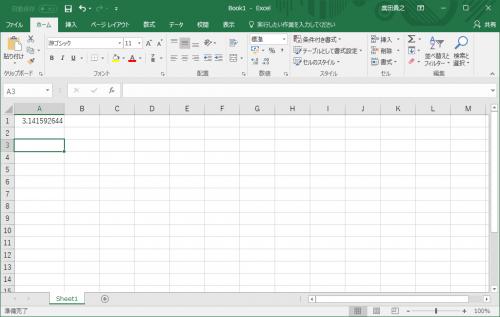
実行結果
マクロを記述するウィンドウの「Sub」と「End Sub」の間にカーソルを置いて、画面上方の再生ボタン的なアイコン(右向きの三角形)をクリックするか、[F5]キーを押して実行します。
いやあ、nがたったの1億なのに、かなりの精度ですね。
3.141592644ですよ。
わたしが覚えている円周率は3.14159265358979323ですから、小数第7位まで合ってますよ。
正直、nがたった1億でここまで合うと思っていなかったので、かなり驚いています。はい。
ただ、1億もの項の計算、人間の手では無理ですよね。さすがExcelです。
Excelは便利
悔しいですが、Excelは便利です。
Microsoftにお金を払うのは癪でしょうがないんですが、Excelばかりは仕方がない。
マクロを書くようになると、Excelからは離れられないですね。
30日間、残り10日です。頑張ります。