16日目 最大公約数を求めよう【30日間1日1本マクロ生活】

30日間1日1本マクロ生活、16日目です。
30日の半分が過ぎ、今日から折り返しです。我ながらよく続いています。
マクロを書く準備は、0日目に記事を書きました。
最大公約数
最大公約数って、小学校で習いますよね。
二つの数字があって、その両方を割り切ることのできる数を「公約数」と言います。
例えば、12と18だったら、
なので、2は12と18の公約数です。
なので、3は12と18の公約数です。
なので、6は12と18の公約数です。
公約数はいくつかあります。その中で一番大きい公約数を「最大公約数」と言います。
12と18の最大公約数は6です。
ユークリッドの互除法
ユークリッドの互除法は高校1年生で学習します。
例えば12と18なら、大きい方の18を小さい方の12で割ります。
割った数12を余りの6で割ります。
この操作を繰り返すと、最後は必ず余りが0になります。
余りが0になったとき、最後に割った数が最大公約数です。
最大公約数1になったときは、この二つの数は1以外に公約数がありません。このようなとき、二つの数を「互いに素」と言います。
「もう約分できない状態」と言えば分かりやすいでしょうか。
例えば25と32。
余りが1になりました。よって、25と32は互いに素です。
マクロを書いてみよう
この「ユークリッドの互除法」を使って、2つの数の最大公約数を求めるマクロを書いてみます。
互除法では、割り算の商は不要です。余りだけが必要。Excelには余りだけ求める便利な計算法がありますよね。
さっそくコードを
Function gcd(m, n)
If m >= n Then
a = m
b = n
Else
a = n
b = m
End If
Do Until b < 1
r = a Mod b
a = b
b = r
Loop
gcd = a
End Function
解説します。
今日もFunction型でやります。
カッコ内にmとnの2つの文字があります。この文字を引数(ひきすう)というのですが、最大公約数を求めるためには2つの数が必要ですよね。
ですから、今回の関数「gcd」は2つの引数を要求します。
大きい方がa、小さい方がb
はじめのIf文は、与えられた2つの引数のうち、大きい方をaに入れ、小さい方をbに入れるという操作です。
厳密には「大きい方がa」ではなく、「小さくない方がa」です。
数学ではこういう言い方をするんですよ。
「大きい方」と「小さくない方」。違いが分かりますか?
互除法
Do Untilから始まるループは、ユークリッドの互除法をマクロで書いたものです。
割る数「b」が1より小さくなるまでループを繰り返します。
割られる数「a」には、さっき割った数「b」を入れます。
割る数「b」には、さっきの余りの「r」を入れます。
これを繰り返すことで、最後の「a」が最大公約数になります。
実行結果
「Sub」型のマクロであれば、マクロを記述するウィンドウの「Sub」と「End Sub」の間にカーソルを置いて、画面上方の再生ボタン的なアイコン(右向きの三角形)をクリックするか、[F5]キーを押して実行しますが、「Function」の場合は実際にワークシートにその関数を書くことができます。
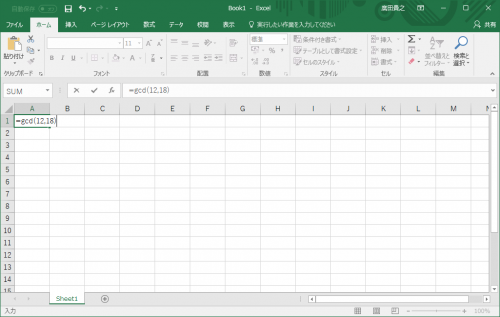
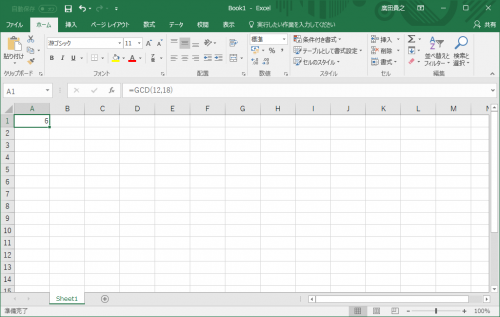
新しく作った「gcd」という関数を入力します。12と18でいきましょう。
はい、正しく「6」と表示されました。
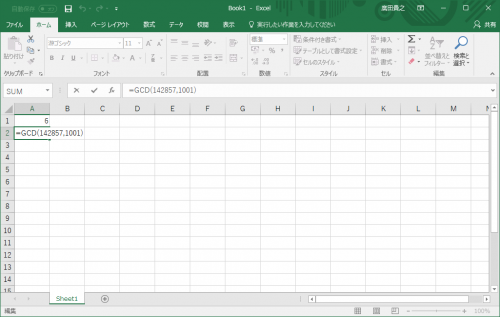
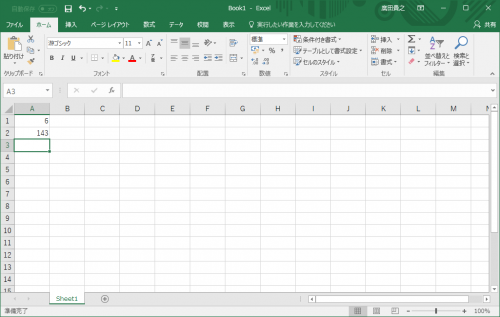
じゃ、142857と1001です。
答えは143でした。
確かに、 です。
Excelは便利
悔しいですが、Excelは便利です。
Microsoftにお金を払うのは癪でしょうがないんですが、Excelばかりは仕方がない。
マクロを書くようになると、Excelからは離れられないですね。
30日間、頑張ります。