高校で勉強した対数は高校生を困らせるだけのものではありませんでした
対数
対数って覚えてますか？
高校の数学で勉強する内容なんですけど、なかなか普段の生活に使う場面ってないんですよね。
高校生の中にも、なんでこんなこと勉強するのかわかんねえ！って思ってるやつもたくさんいると思います。
ていうか、ほとんどだと思います。
ということで、対数について調べてみました。
むかしは計算機がなかった
今は、計算は機械にやらせればいいっていう時代です。
面倒な計算は電卓叩けば即座に答えが出ます。
面倒でない計算ですら、電卓でやってくれます。
はいはい。おめえらは、電卓すら触ったことがないんだね。スマホのアプリで電卓があるだろ。それ使え！
さらに複雑な計算は、パソコンでやらせればいい。Excelにやらせれば、たいていの計算は大丈夫です。
でもね。むかしは計算機がなかったんですよ。
そんな中で、
かけ算を楽にすることを考えたそうな
そこで、前もってこんな表を準備しておいたんだそうです。
| 指数 | 数値 |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
| 7 | 128 |
| 8 | 256 |
| 9 | 512 |
| 10 | 1024 |
| 11 | 2048 |
| 12 | 4096 |
| 13 | 8192 |
| 14 | 16384 |
| 15 | 32768 |
| 16 | 65536 |
この表の、右の欄の「数値」の方からさっきの「64」と「256」を探すんです。
すると、その左の「指数」の所には「6」と「8」が書いてありますよね。
その数字をたし算するんです。明らかに、かけ算よりもたし算の方が簡単に計算できますよね。
6と8をたして14。その14を指数の方から探すと、数値の方には16384と書いてあります。
そう。
これが対数の考え方なんですよね。
かけ算をたし算にすることを考えた
対数を考えたのは、むかしむかしの数学者のネイピアさんって人なんですけど、この人はかけ算をたし算にすることを考えたんです。
さっきの表では、数値の欄にかなり飛び飛びの数字しか書かれてなかったので、まったく使い物になりませんが、これのすごく精密なやつを作り出したんです。
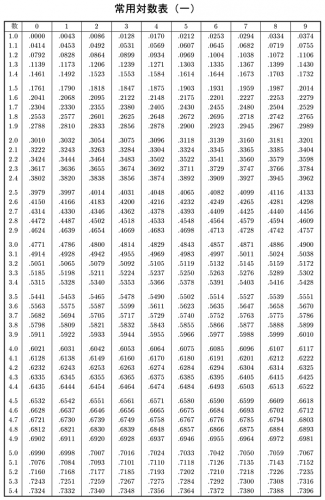
高校の数学の教科書に載っている「常用対数表」っていう表の一部です。
例えば、一番左の2.0っていう行には、横にずらりと4桁の数字が10個並んでますよね。これが順番に2.01、2.02、2.03、・・・2.09に対応してるんです。
2.73だったら0.4362、1.41だったら0.1492。これをたして0.5854です。
0.5854を表の中から探すと、3.85の所に0.5855があります。
よって、
ちなみに、実際にこのかけ算をやってみると3.8493。ほぼ正解です。
天文学者の寿命を倍にした
対数の発明により、かけ算の計算は強力に簡単になりました。
とんでもなく大きな数字を「天文学的数字」なんて言い方をしますよね。
天文学者は大きな数字を本当に手作業で計算していたんでしょう。電卓の無かった時代に、気の遠くなるような大きな数字の計算をしていたんだと思います。
対数の発明により、天文学者の寿命が倍に伸びた、と言われるほど、対数がかけ算の計算を楽にする効果は抜群でした。
書き方
ということで、作法です。
という表現になります。この 
上の数値の例でいうと、
いまの時代に必要か
いまの時代は、ITの時代。計算は機械がやってくれます。
かけ算だろうが、たし算だろうが、機械にやらせれば時間はかかりません。
じゃ、いまの時代に対数は必要なんでしょうかねぇ。
答えはもちろん、Yesです。
はじめはかけ算を楽にするために作られたものかもしれませんが、今では別の用途がたくさんあるんです。
数学の世界では、対数がなくなるなんて考えられないことです。
何よりも、対数がなくなったら、対数の計算ができなくなるじゃないですか。こんなに楽しいのに。
・・・って考えるのが数学奇人なんです。