間違えて約分しても正解できます

2020年12月5日

1129032258064516

先日、すごい数を見つけたんです。上の見出しの数なんですけど。

1129032258064516です。16桁の数ですね。

7倍してみましょう

この数、7倍してみましょう。

16桁です。その辺の電卓では桁があふれます。

Excelで計算させても、まじめにやってくれません。

7.90323E+15

ほら。全くやる気がありません。

だから、手作業でやりましょう。

わたしですか？もちろんやりましたよ。やったにきまってるじゃないですか。

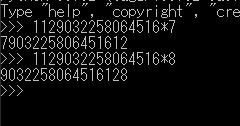
答えは7903225806451612です。

8倍してみましょう

今度は8倍してみましょう。

電卓やExcelが頼りにならないのはもう分ってますよね。

わたし？もちろんやりましたよ。決まってるじゃないですか。

答えは9032258064516128です。一瞬です。暗算です。

不正発覚

あ・・・

このことはくれぐれも内密に・・・

何がすごいのか

これって、何がすごいのかって言うと。

そもそも、1129…という同じ数を7倍、8倍したんだから、
$\dfrac{1129032258064516 \times 7}{1129032258064516 \times 8}=\dfrac78$
ですよね。当然です。

で、実際に7倍、8倍を計算した結果をそのまま分数で書くと

$\dfrac{1129032258064516 \times 7}{1129032258064516 \times 8}=\dfrac{7903225806451612}{9032258064516128}$

ってなるんです。

7903225806451612／9032258064516128って、赤い部分の数字が全く同じなんですよ。

だから、分数を勉強して間もない小学生なんかが、間違ってこの部分が同じだから約分して消しちゃったとしても、答えが $\dfrac78$ で、合っちゃうんです。